Câu 1. Cho hàm số:

$y = \frac{{2x + 1}}{{x + 1}}$

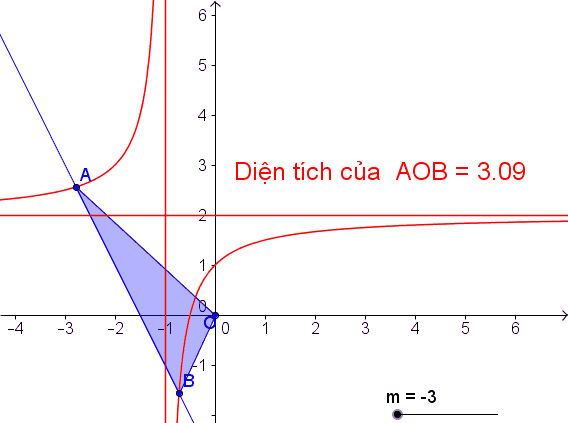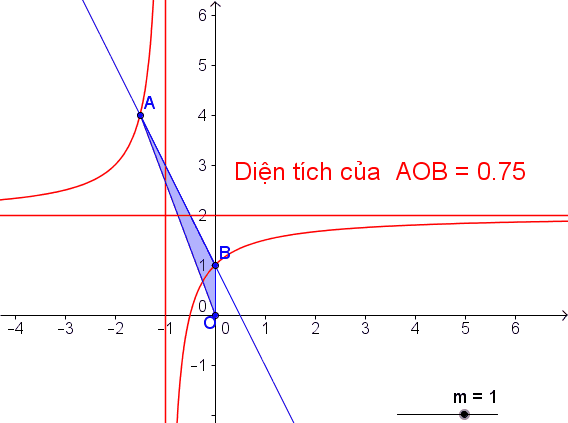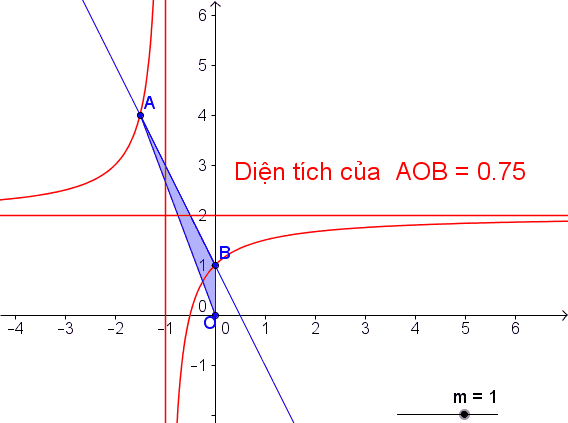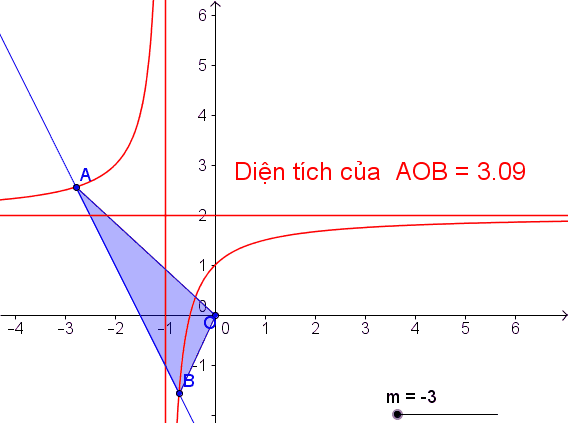
Tìm m để đường thẳng y = -2x + m cắt đồ thị (C) tại hai điểm phân biệt A và B sao cho tam giác OAB có diện tích bằng $\sqrt 3$ ( O là gốc tọa độ)

Phương trình hoành độ giao điểm:

$\frac{{2x + 1}}{{x + 1}}= - 2x+m$

$\Leftrightarrow 2x + 1 = (x + 1)( - 2x + m)$ (do x = -1 không là nghiệm của phương trình)

$\Leftrightarrow 2{x^2} + (4 - m)x + 1 - m = 0\,\,(1)$

$\Delta ={m^2}+8> 0$ với mọi m, suy ra đường thẳng y = -2x + m luôn cắt đồ thị (C ) tại hai điểm phân biệt A, B với mọi m.

Gọi $A({x_1};{y_1})$ và $B({x_2};{y_2})$ trong đó là các nghiệm của (1);

${y_1}=-2{x_1}+m$ và ${y_2}=- 2{x_2}+m$

Ta có:

$d(O,AB) = \frac{{\left| m \right|}}{{\sqrt 5 }}$

và

$AB=\sqrt{{{({x_1} - {x_2})}^2}+{{({y_1} - {y_2})}^2}}$

$=\sqrt{5{{({x_1} + {x_2})}^2} - 20{x_1}{x_2}}=\frac{{\sqrt {5({m^2} + 8)} }}{2}$

${S_{OAB}}=\frac{1}{2}AB.d(O,AB)=\frac{{\left| m \right|\sqrt {{m^2} + 8} }}{4}$ ,

Suy ra:

${S_{OAB}} = \frac{1}{2}AB.d(O,AB) = \frac{{\left| m \right|\sqrt {{m^2} + 8} }}{4}$

, suy ra:

$\frac{{\left| m \right|\sqrt {{m^2} + 8} }}{4}=\sqrt 3\simeq 1.73$

$\Leftrightarrow m=\pm 2$

Bình luận về bài viết này Hủy trả lời

Chuyên mục